算法复杂度
June 3, 2022
Time complexity #
时间复杂度
算法执行所需的操作数,而不是实际的运行时间
当输入 n 足够大时,低阶项可以被舍弃
RAM #
Random Access Machine
- 单处理器
- 指令按序处理,无并发操作
- 仅包含常用指令,每个指令的执行占用常量操作时间
Average case #
对 size n 的 平均 输入,算法执行所需的操作数,(平均运行时间)
通常要用到概率分析的方法,取决于输入的分布,如果没有合理的输入分布,我们不能用概率去分析
Worst case #
对 size n 的任意输入,算法执行所需的最大操作数,即运行时间的 上界 (上限)
使算法执行时间最长的输入,例如对插入排序而言,待排序数组是已经反向排序好的
最常用
Best case #
使算法执行时间最短的输入,例如对插入排序而言,待排序数组是已经正向排序好的
\( \Theta \) notation #
\( \Theta(g(n)) = \{f(n): \exists c_1, c_{2}, n_{0} \in \mathbb{R^{+}} , \forall n_{0} \leq n, 0 \leq c_{1}g(n) \leq f(n) \leq c_{2}g(n) \} \)
\(f(n) = \Theta(g(n))\),即 \(f(n) \in \Theta(g(n))\),\(f(n)\) 为集合 \(\Theta(g(n))\) 中的一员
\(\Theta(g(n)) \subseteq O(g(n)) \)
算法 最坏运行时间 的紧界,不能表示对 任意 输入算法运行时间的紧界
定理:对函数\(f(n), g(n)\)而言,当且仅当 \(f(n)=O(g(n))\), \(f(n)=\Omega(g(n))\) 时, \(f(n) = \Theta(g(n))\)
\(O\) notation #
\( O(g(n)) = \{f(n): 存在常量 c, n_{0} \in \mathbb{R^{+}} , \forall n_{0} \leq n, 0 \leq f(n) \leq cg(n) \} \)
大 \(O\) 表示法,表示对大小为 n 的 任意 输入,算法运行时间的 上界
\(\Omega\) notation #
大 \( \Omega \) 表示法,表示对大小为 n 的 任意 输入,算法运行时间的 下界
对 size n 的任意输入, 最好运行时间 的下界;例如对插入排序而言,元素都是已经排序好的情况下
\(o\) notation #
小 \(o\) 表示法,跟 大\(O\)的区别为,对任意常量 c
不紧的上界,要低一个阶
例如:\(2n = o(n^{2}) \),但 \(2n^{2} \neq o(n^{2}) \)
\(\omega\) notation #
小 \(\omega\) 表示法
不紧的下界,要高一个阶
图例 #
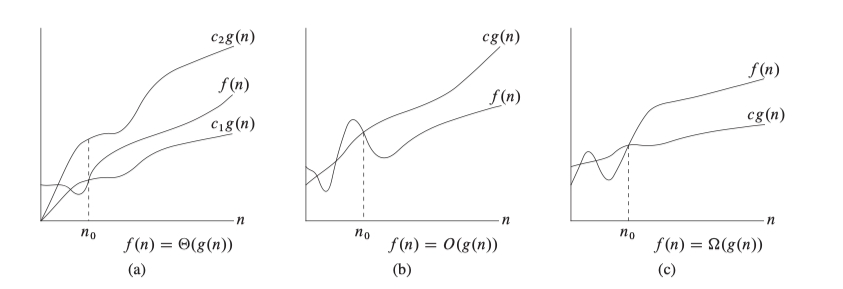
\(n_{0} 为最小可能值\)
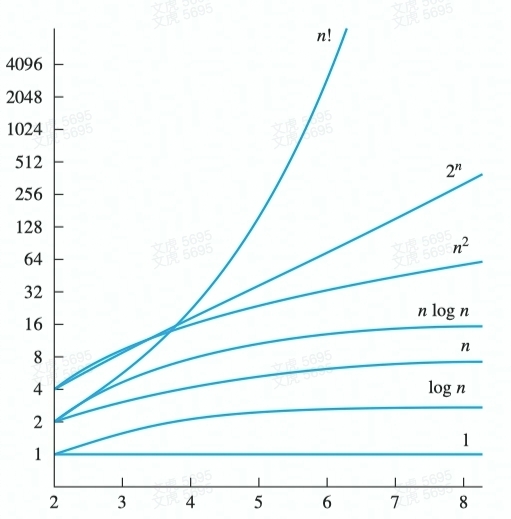
常用函数增长曲线
Space complexity #
空间: 内存
空间复杂度:算法输入所占据的内存 + 辅助内存
Space Complexity = Auxiliary space + Space used by input values
Recursive call stack,递归调用栈也算空间占用
空间复杂度跟实现算法所使用的数据结构有关
Auxiliary space #
辅助空间: 算法执行需要的额外空间